If you never take a chance, you’ll never win. Continue reading →

Vi! Maths was never so fun! Continue reading →

The Times has a great series of essays by Errol Morris on Thomas Kuhn’s The Structure of Scientific Revolutions. According to the author, Structure is a post-modern work which makes the relativist claim that people in one paradigm (or culture … Continue reading →

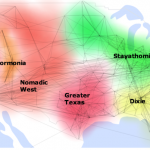
Marvellous visualization of where friends tend to cluster in Facebook. Apparently everyone in Dixie knows someone in Atlanta and all the Mormons are friends with each other. My latest visualization shows the information by location, with connections drawn between places … Continue reading →

Regular readers know that I am a big fan of Better Explained in which Kalid makes mathematical ideas accessible. Today’s installment: Integration is just multiplication when one of the operands is changing. Most people grok integration as area under a … Continue reading →

Whereas the constitution sets clear boundaries on the authority of the Federal government. Whereas the federal government has no business defining basic mathematical constants. Resolved, that theories, definitions and celebrations of Π should be left to the various States.

Last time I visited Better Explanations, I got stuck there for hours. I resisted this time once I realized I was reading all the same articles for a second time. Today’s bait showed up in my RSS feed. Suppose we … Continue reading →

Clearly Kate is much too smart to make a mistake like that. Continue reading →

Ever wondered why there are 360 degrees? Constellations make a circle throughout the year — ever see the Big Dipper upside down sometimes? (Never fear, it’ll be rightside-up in 6 months). Here’s a theory about how degrees came to pass: … Continue reading →

To save you going all the way to Project Euler to read it, I have copied problem 12 here for your puzzle solving convenience… The sequence of triangle numbers is generated by adding the natural numbers. So the 7th triangle … Continue reading →